INTERPOLATE transforms (disaggregates) a lower-frequency timeseries to a higher-frequency timeseries, for instance converting annual data to quarterly data, optionally using a higher-frequency indicator series (use COLLAPSE to perform the inverse transformation). The statement ignores the global time period, and a local time period cannot be set.

Instead of the INTERPOLATE statement, you may alternatively use the similar interpolate() function, for instance x!a.interpolate(); (see under functions).

Syntax

interpolate < print > highfreq = lowfreq indicator method indicatormethod;

highfreq	Higher frequency timeseries. Frequency can be indicated with suffix !a, !q, !m or !w. Banknames may be used. Lists of names can be used, like for instance {#m}.
lowfreq	Lower-frequencey timeseries. Frequency can be indicated with suffix !a, !q or !m. Banknames may be used. Lists of names can be used, like for instance {#m}
indicator	(Optional). A high-frequency indicator series to aid the construction of the resulting timeseries, by providing the seasonal patterns. When using an indicator, choose between the olsette, cholette or denton methods.
method	(Optional). Choose between: •total: The sum of the high-freq values is equal to the low-freq value. Example: an annual value of 100 will be split into four quarterly values of 25 each. •avg: The average of the high-freq values is equal to the low-freq value. Example: an annual value of 100 will be split into four quarterly values of 100 each. •(repeat: Obsolete: use avg.) •(prorate: Obsolete: use total.) Note: if no method is indicated, default is avg. You can alter the default with option interpolate method = ... ; (cf. OPTION).
indicatormethod	(Optional). When using an indicator, choose between these metods, all of the "Denton family": •olsette: Unless you have very few observations in the low-frequency series, this is the recommended method to use with an indicator series. The method is more foolproof than both the cholette and (especially) the denton methods. With olsette, the collapsed high-frequency indicator series is first collapsed into a low-frequency indicator, which is OLS-fitted on the low-frequency series (+ a trend and a constant term), following which an adjusted low-frequency indicator series is constructed. The adjusted indicator series is then used instead of the "real" indicator series, using the Cholette method. The Olsette method is invariant regarding the relative and absolute levels of the high-frequency indicator versus the low-frequency series. The method may fail with an OLS error if for instance the OLS algorithm has too few degrees of freedom (too few low-frequency observations), and also -- but much more rare -- if the indicator series collapses exactly into a constant series (in that case, OLS also fails). Use option interpolate olsette trend = no; to switch off the trend in the OLS estimation. •cholette: The Cholette method is essentially an "improved Denton", fixing the Denton problem of spurious movements in the beginning of the resulting series, if the levels of the low-freq and indicator series do not match. The method tries to minimize the absolute changes in differences between the indicator series and the resulting series, while preserving total- or avg-aggregation. The Cholette method is invariant regarding absolute levels of the high-frequency indicator versus the low-frequency series (but it is not invariant regarding the relative levels of the high-frequency indicator versus the low-frequency series). •denton: This is the original Denton method, cf. this paper (reproduces the delta(x-z) column on page 101). The Denton method is sensitive regarding the relative and absolute levels of the high-frequency indicator versus the low-frequency series. So in general, use olsette or cholette rather than denton, because with Denton, you risk spurious movements at the start of the resulting series. Denton should only be used if Olsette/Cholette uses too many computer ressources, which would only happen with extremely long timeseries. When using an indicator, you must at the same time choose both a method and an indicatormethod, for instance interpolate x!q = y!a indicator=z!q avg cholette;. Note that during calculations with indicators, no matter TIME settings or local <...> period, the method will always use the longest possible period where there is data for both the low-frequency and high-frequency input series. In the interpolate() function variant, TIME or <...> period only affect which periods are updated after the calculation is performed.)
print	(Optional). When using an indicator together with the olsette method, the OLS regression is printed on the screen for the user to inspect. With many INTERPOLATE statements, this option will slow down Gekko considerably due to the printing.

•If a variable without databank indication is not found in the first-position databank, Gekko will look for it in other open databanks if databank search is active (cf. MODE).

•Looping: with a list like for instance #m = x1, x2;, you may use interpolate {#m}!q = {#m}!a; to interpolate x1!a into x1!q, and x2!a into x2!q.

Examples

Use this to convert frequency:

reset; time 2018 2020;
x!a = 2, 3, 4;
interpolate x!q = x!a;
prt <n> x!a, x!q;

Since the method is avg as default, this will create the quarterly timeseries x!q where each quarterly observation in x!q is the same as the corresponding annual observation in x!a. Alternatively, you use total option (interpolate x!q = x!a total;). Now, the quarters will sum up to x!a instead of just being repeated.

Note that when interpolating from a, q or m frequency into w (weeks), the weeks at the start/end will often become missing values, when the weeks do not fit exactly inside the years, quarters or months. Consider this example:

reset; option freq m; time 2017m1 2017m2;
x!m = 1;
interpolate x!w = x!m total;
option freq w; time 2016w52 2017w9;
prt<n> x!w;
prt sumt(<2017w1 2017w8>, x!w); //1.8963

// x!w
// 2016w52 M //6 missing days
// 2017w1 0.2258

// 2017w2 0.2258

// 2017w3 0.2258

// 2017w4 0.2258

// 2017w5 0.2431

// 2017w6 0.2500

// 2017w7 0.2500

// 2017w8 0.2500
// 2017w9 M //5 missing days

The data for the months 2017m1 and 2017m2 are interpolated into the weeks 2016w52-2017w9. Week #52 of 2016 actually contains January 1, 2017 (a Sunday), but since the six previous days of that week are missing (December 26 to December 31, 2016), the interpolation sets 2016w52 to missing values. Similarly, week #9 of 2017 contains the days February 27 and February 28, but the five subsequent days are missing. The sum is not exactly 2, because one day of January and two days of February are "spilled" (1.8963 = 2 – 1/31 – 2/28). (Weeks are defined and numbered following the ISO 8601 standard, where days around New Year may belong to week 52, week 53 or week 1. Active 'workdays' will be implemented, omitting for instance weekends and holidays. For now, see the getSpecialDay() function).

Olsette/Cholette

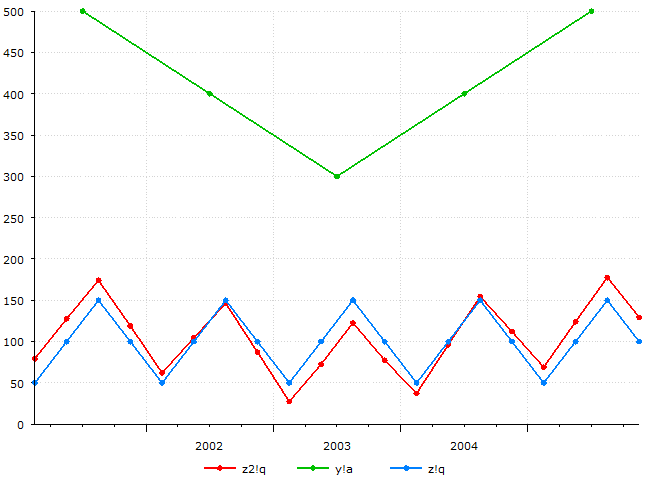
The following is an example of using the Cholette method. (Note: changing the method to olsette here will result in an error, because the collapsed indicator is a constant annual series with value 400, which makes the OLS regression fail. Changing the method to denton gives almost the same result, because the series are well aligned level-wise).

//Cf. example Denton: Adjustment of Monthly or Quarterly Series to Annual Totals: An Approach Based on Quadratic Minimization (https://www.oecd.org/sdd/21779760.pdf). The results below differ a tiny bit from

the values in the article, because the Cholette method is used here. To reproduce exactly, use

"interpolate z2!q = y!a indicator=z!q total denton;"

reset;
time 2001 2005;
y!a = 500,   400,   300,   400,   500;
z!q = 50, 100, 150, 100,  50, 100, 150, 100,  50, 100, 150, 100,  50, 100, 150, 100,  50, 100, 150, 100;
interpolate z2!q = y!a indicator=z!q total cholette; //Or: z2!q = interpolate(y!a, z!q, 'total-cholette');
p <n> z2!q.collapse(), y!a, z!q.collapse(); //Shows that z2!q sums up to y!a, but z!q does not.
prt <n> z2!q; //z!q.collapse() should be comparable to y!a levels!

--> result:
   z2!q

2001

q1 79.2980

q2 127.5788

q3 174.1404

q4 118.9828

2002

q1 62.1060

q2 104.5129

q3 146.2034

q4 87.1777

2003

q1 27.4355

q2 72.5645

q3 122.5645

q4 77.4355

2004

q1 37.1777

q2 96.2034

q3 154.5129

q4 112.1060

2005

q1 68.9828

q2 124.1404

q3 177.5788

q4 129.2980

clip0163

The above can be exactly reproduced with the tempdisagg package in R:

library(tempdisagg)
d.q <- ts(rep(c(50, 100, 150, 100), 5), frequency = 4)
d.a <- ts(c(500, 400, 300, 400, 500))
a1 <- predict(td(d.a ~ 0 + d.q, method = "denton-cholette", criterion = "additive", h = 1))
print(a1)

--> result:

Qtr1 Qtr2 Qtr3 Qtr4

1 79.29799 127.57880 174.14040 118.98281

2 62.10602 104.51289 146.20344 87.17765

3 27.43553 72.56447 122.56447 77.43553

4 37.17765 96.20344 154.51289 112.10602

5 68.98281 124.14040 177.57880 129.29799

Note

If a frequency indicator is omitted, Gekko will use the current frequency.

Interpolate with total option and collapse with total option are in a sense mirror images, and for example for an annual timeseries x!a, x!a.interpolate('total') will disaggregate into quarters, and x!a.interpolate('total').collapse('total') will aggregate the quarters back to the original annual series (this identity does not work if you are interpolating to and collapsing from weekly data).

The olsette method is named both after OLS and Jes Asger Olsen.

Related options

OPTION interpolate method = repeat; [total|avg]

OPTION interpolate olsette trend = yes; [yes|no]

Related statements

COLLAPSE, SMOOTH